#学习笔记
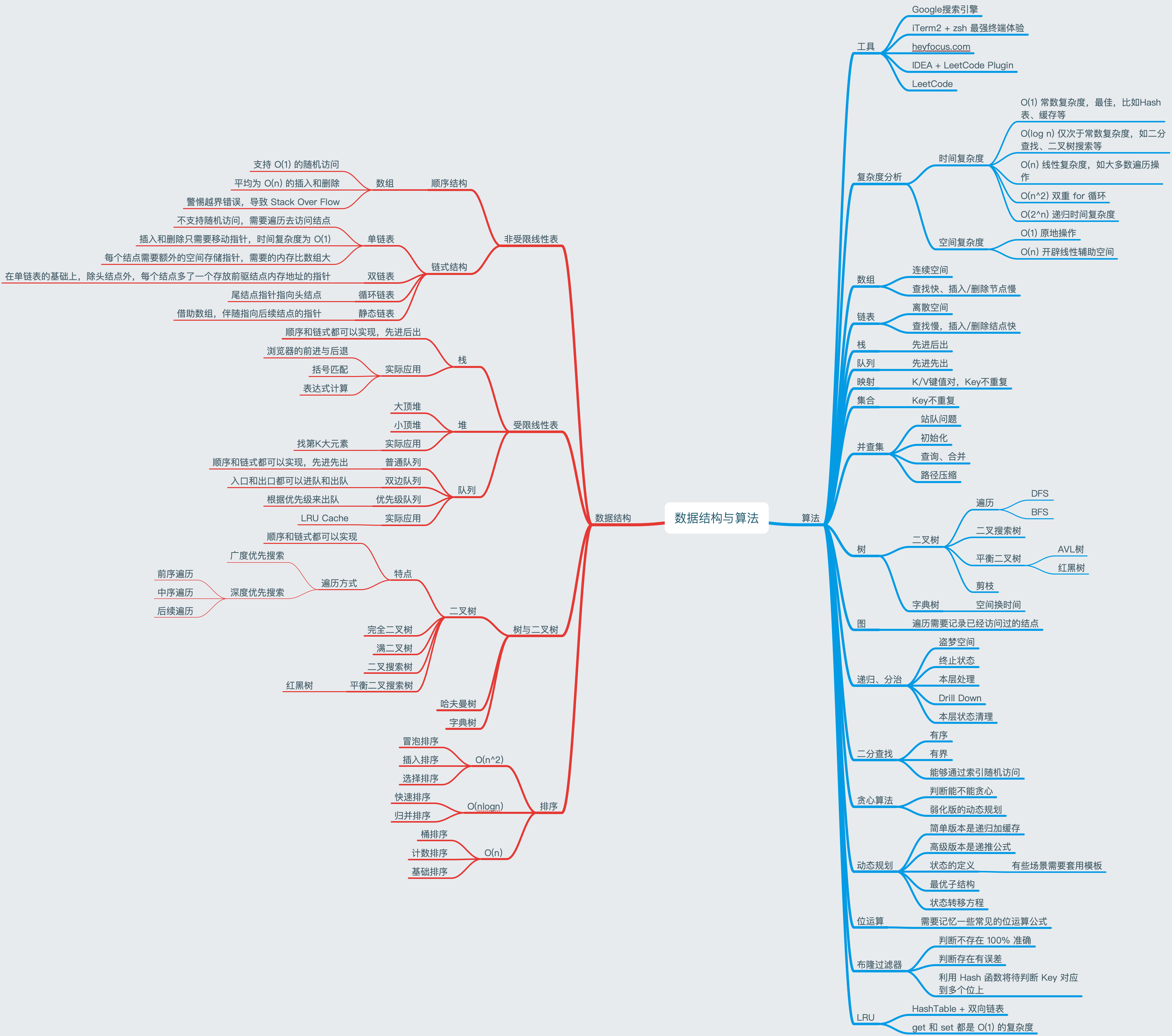
##第1课 | 数据结构与算法总览
- 上课之前要把课程预习和查看一遍
- 学习过程中首先要注重预习
- 基础知识自己预习和查看
- 跟着老师一起思考、回答问题
- 一定坚持按照切题办法来把课后作业完成
- 书名:《异类:不一样的成功启示录》
- 想精通任何一个领域,分三步
- Chunk it up 切碎知识点
- 把算法和数据结构这样比较大比较繁复的知识体系,切成一块一块相对比较明确的脉络化的一个知识脑图,他们必须是脉络相连的。
- 任何知识体系都是一颗树,叫做语法树。人脑适合记忆和理解孤立的知识。所以一定要把它弄成一个脑图。
- 要想要达成职业水平,把每一个部分单独挑出来练习,这样经过很多次不断地反复练习和刻意练习,最后能够达到顶尖的水平。
- 所有的复杂的算法,最后其实就是找它的重复单元是什么。
- 任何高级算法和数据结构,到了最后都会转换成if eles 或者是for loop 或者是递归
- 都会转换成if eles 或者是for loop 或者是递归
- Deliberate Practicing 刻意练习
- 要成为顶尖水平的话,最关键的一点就是所谓的基本功。
- 基本功是区别业余选手和职业选手的根本。
- 基础动作的分解训练和反复练习。
- 关键就是能够把基础动作进行分解训练。
- 最大的误区就是如果做一个算法题,只做一遍,那么这就是你进行练习和切题的最大误区。
- 刻意练习-过遍数(五遍刷题法)
- 刻意练习就是要练习弱项,自己实力上缺陷的地方。==
- 一只脚踏在舒适区之外,把自己的弱项进行反复练习。
- 切题如果一直犯糊、没有头绪,那么就逼自己反复练习这些。
- 正是应为这种大量反复练习,最后才能使基本功变好。
- 关键是练基本功,基本功练好了之后才能体会到现实当中,比如工程化的时候应该怎么做。
- 在进行算法和数据结构练习的时候,就是一些很典型的题目,然后不断地练习,一个题目举一反三,把不同的算法、不同的数据结构过遍数练习好了之后,这就是所谓刻意练习带来的基本功的一个提升。
- 要客服自己的理解的一个误区,别只想做一些高大上的框架、学习一些高大上的技术、把基础全部都练习好之后真正写工程代码就会事半功倍。
- Feedback 反馈
- 主动式反馈(自己去找)
- Github、LeetCode上面写的好的代码。
- 被动式反馈(高手指点)Code Review
- 刷题具体技巧
- 五遍刷题法所谓的五毒神掌
- 对于单个题目的话,在写任何一个题目之前养成四步统化的方式,简称切题四件套。
- Clarification:指的是和面试官以及你自己多看几次题目,和面试官反复沟通一下这个题目,确保自己对这个题目的理解是正确的。
- 题目没看清楚就开始解答和开始写程序,经常会犯一些很知名的错误。
- Possible solutions
- 当看到一个题目之后,要做的一件事情就是,想所有可能的解法来解这个题目。
- compare(time/space)不要只用到想到的第一种解答去解,要把所有可能的想法首先先过一遍,同时比较不同的方法,他们的时间和空间复杂度。
- optimal(加强)养成思维习惯,把每一个不同解法它的时间和控件复杂度学会分析,从中找出最优的一种解法,最优的解法一遍就是时间最快的一种解法。
- Coding(开始写代码)
- Test case 写完代码之后把测试样例能够列举几个,测试自己的程序是否正确,给面试官一个感觉就是有始有终。
- 五遍刷题法 任何一个题目要做五遍或至少做五遍
- 先花五分钟时间读题和思考,把题目的意思理解了。
- 如果基础比较薄弱的话,可以给自己十分钟,最多十五分钟的时间进行读题和思考。
- 有思路就开始做,要是这十分钟到十五分钟没有任何思路的话,直接看解法。
- 算法本身的话是要理解学习和运用一个算法,而不是自己去发明创造。
- 一般题型有多种解法,比较不同解法的优劣。
- 把每个解法背诵和默写好,背诵和默写很重要。
- 虽然并不是完全死记硬背,但是先把它背诵和记住了之后,一般都可以理解,只是要反复很多遍之后,看到类似的题才能够很快写出来,以及得到它的思路。
- 第一遍直接看解法,不要再纠结。
- 直接看解法即可,然后背诵默写好的解法。
- 马上自己写,不要再看别人的代码以及解法,闭卷进行考试,开一个浏览器,一个空白的文件,在里面开始吧代码自己写出来,写完之后放在LeetCode上面跑写的程序,然后debug修改,debug修改,直到通过为止。
- 一道题有多种解法,每种解法的话都写一遍,直到通过。
- 每种解法在LeetCode上面还会有不同执行时间和内存消耗,最重要的就是执行时间,不同解法比较它们的执行时间,同时对于同一种解法,执行时间太长想象优化的办法,直到这些不同的解法都能通过,而且执行时间是相对比较优的。
- 过了一天后,再回过头来做之前前一天做过的题目。
- 不同解法的熟练程度要是不一样的话,对自己不是特别熟练的那些题进行专项训练。
- 注意这里就是过了一天之后,马上再反过来进行练习。
- 4.过了一周之后反过来练习相同的题目,同时对于自己不熟练的题目再进行专项练习。
- 前四遍得到的效果就是对这一类题会比较熟练。
- 如果有面试的话,面试前一周恢复性训练,再把之前做过的题重新做一遍,可按照自己的时间安排。
- 总结
- 拆分知识点、刻意练习、反馈。
##第2课 | 训练准备和复杂度分析
###1. 训练环境设置、编码技巧和Code Style
- 电脑设置
- Chrome默认搜索引擎一定要设置为Google。
- Terminal 2 和 zsh
- 一站式IDE :VSCode、Java:IntelliJ、Python:Pycharm
- LeetCode Plugin
- 中文网站 leecode-cn.com 和 英文网站leetcode.com
- 任何中文站的题目和国际站的题目,它的地址后半部分都是相同的,最关键就是前面没有-cn,任何一道题目只要把前面的-cn去掉之后就可以来到国际站,题目是一模一样的,最关键的就是它的Discuss不一样。
- 国际站最好的地方在于,外国友人贡献了很好的思路和很好的代码学习。
- 做题的时候以中文站为主,写过之后或者遇到问题的时候,一定要在国际站的讨论区里面,按照most votes排序之后,看下最高票的答案和最高票的回答,这些回答是全球最牛逼的程序员智慧结晶,一般把前三个回答都看了。
- Code Style :Java、Python
- Google、Facebook、Airbnb
- 一线互联网公司其实都是配好了的,IDE里面就是公司统一的Code Style。
- if 后面一定要有空格,左括号前面一定要写空格,左括号不用另启一行,直接跟在后面就行了。
- 所有的括号和关键字前后都要有空格,另外运算符,加号减号前面都要有空格。
- 指法和小操作
- home行头,end行尾:command + left / rigjt
- 单词分切:option + left / right
- 删除delete:删除光标右侧:Fn+delete 删除单词option + delete
- 选中整行(光标在行头时)shift + command + right
- 选单词、整个单词调位置以及选整行。
- IDE的自动补全功能。intelliJ :option + return自动补全、commend + E已经访问过的文件左右跳
- 对于一个新上手的IDE,一定要刻意练习,把IDE的Top tips在网上搜索使用技巧。
- 工欲善其事必先利其器。
- 养成习惯,逼自己进行所谓工具和配置环境的刻意化练习。
- 自顶向下的编程方式。
- 回文串:从右到左和从左到右都是一个串,都是一样的字符串。
- 看到一个题目之前一定要反复审题,特别是边界条件问题。
- 自顶向下如何编程
- 自顶向下的编程方式指的是,在思考一个问题的话,最开始就是思考大层次的逻辑,而不要纠结它的细节,就是以高层次主干逻辑为主。
- 自顶向下的协作方式不纠结方法的具体细节,而把主干的逻辑先用代码写出来,写的时候虽然这些方法没有实现,后续再来专注写这些代码本身。
- 日常工作中写工程型代码会隔年的游刃有余,工程型代码业务扩机代码相对来说比较冗余比较繁琐,冗余的逻辑一层一层下来,那么要写代码写的快同时Bug少的话,关键是先解决最上层的主干逻辑。
- 自顶向下编程的写代码方式可读性强,而且不容易犯错。
###2. 时间复杂度和空间复杂度分析
- 它的复杂度是n的怎样的一个函数
- 时间复杂度Big O notation 、空间复杂度。
- O(1): Constant Complexity 常数复杂度
- O(log n): Logarithmic Complexity 对数复杂度
- O(n) Linear Complexity 线性时间复杂度
- O(n^2): N square Complexity 平方
- O(n^3): N cubic Complexity 立方
- O(2^n): Exponential Growth 指数
- O(n!): Factorial 阶乘
- 注意:只看最高复杂度的运算
- 怎么来看一个时间复杂度?
- 直接看这个函数或者这段代码,它根据n的不同情况会运行多少次。
- 在写程序的时候,一定要对自己程序的时间和控件复杂度有所了解,而且是养成习惯,写完了之后能够下意识的分析出这段程序的时间和控件复杂度。
- 能够用最简洁的时间和控件复杂度完成这段程序是一个顶尖职业选手的必备的素养。
- 递归如何分析复杂度?关键要了解它的递归总共执行了语句多少次。
- 把递归它的执行顺序,画出这么一个树型结构,称之为它的递归状态的递归树。
- Fibonacci数列的第n项,递推公式:F(n) = F(n-1)+F(n-2)
- 一定不要在面试中直接用数学公式写,可以加一个缓存,把这些中间结果能够缓存下来,或者是直接用一个循环来写。
- 重要:主定理其实是用来解决所有递归的函数,怎么来计算它的时间复杂度。
- 任何一个分治或者是递归的函数,都可以通过主定理算出它的时间复杂度。
- 一般各种递归情形,有四种情况。
- 二分查找: 一般发生爱一个数列本身有序的时候,要在有序的数列里找到你要的目标数,所以每次都一分为二,只查一边,最后时间复杂度是log(n),所以二分查找它是log(n)的时间复杂度。
- 2.二叉树的遍历为O(n),因为通过主定理可以知道它每次要一分为二,但是每次一分为二之后,每一边它是相等的时间复杂度这么下去,最后他的运行时间为O(n)的。
- 二叉树的遍历有一个简化的思考方式,就是二叉树遍历,我们会每次一个节点都访问一次,且仅访问一次,所以它的时间复杂度就是O(n)的。
- 二维矩阵:如何在一个排好序的二维矩阵中进行二分查找?
- 同理用主定理可以得出,最后时间复杂度是O(n)的。
- 如果是一维的数组进行二分查找,就是logn。如果是二维的有序的矩阵进行查找,同理这时候被降了一维就不是n^2的算法,而是O(n)的算法。
- 归并排序Merge sort :所有的排序最优的办法就是nlogn的,所以的话归并排序也是nlogn的时间复杂度。
- 二叉树遍历- 前序、中序、后序:时间复杂度是多少?
- 时间复杂度是O(n)的,这里的n代表二叉树里面的树的借点总数,为什么?通过主定理得到的。
- 方便的一种分析方式:不管是前序、中序、后序它遍历二叉树的时候,每个结点会访问一次且仅访问一次,所以它的时间复杂度就是线性于二叉树的节点总数,也就是O(n)的时间复杂度。
- 图的遍历:时间复杂度是多少?
- 图里面每一个节点访问一次且仅访问一次,所以它时间复杂度为O(n)。这里的n的话是图里面的节点总数。
- 搜索算法:DFS深度优先、BFS广度优先时间复杂度是多少?
- 不管深度优先广度优先,因为访问的节点是访问一次,所以它的时间复杂都是O(n)的,这里的n指的是搜索空间里面的节点总数。
- 二分查找:时间复杂度是多少?
- log(n)就是二分查找的时间复杂度。